图解平方求和公式

连续自然数的平方和，可以用公式 ((2n + 1) / 3 x (n x (n+1) / 2)即n x (n+1) x (2n+1) / 6来求解，那么为什么可以这样来求和呢？因为网页不方便写分数形式的公式，这里就用图片的形式来表达一下：

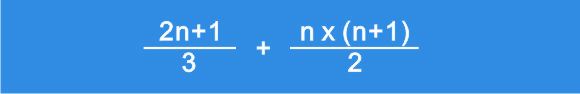
聪明的数学家发现，平方求和的公式可以用几何图形来表现，求1平方至5平方的和，可以绘制成这样一个三角形的阵列，三角形阵列中所有数字之和，就是题目的解；

神奇的是，把三角形分别旋转120度和240度之后，三个三角形任意位置的数字之和都相等；

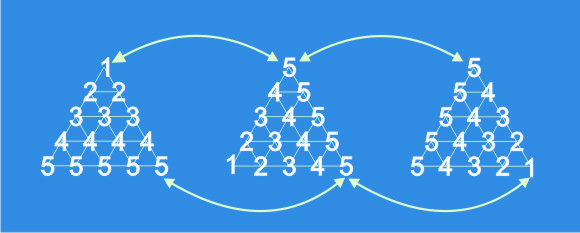
将这三个三角形的相同位置的数字叠加，就得到了这样一个新的三角形，因为之前只是旋转了三角形，所以原三个三角阵列的和都是相同的，而新的三角形的和，是原有任一三角形的3倍；

这就是2n+1的来源，假设3角形阵列有n行，新的三角形的每一项的值都是2n+1，但是因为我们只是求一个三角形阵列的总和，所以我们还需要除以3。也就是（2n+1）/3，至于n x (n+1) / 2，这是求三角形阵列项数的项数公式。知道了每一项的值，也求出了项数，我们就可以很轻松的求出该阵列的总和了。