c++利用递归来计算斐波那契数列某一项的值

有这样一个有趣的“兔子问题”：“假定一对大兔子每月能生一对小兔子，且每对新生的小兔子经过一个月可以长成一对大兔子,具备繁殖能力，如果不发生死亡，且每次均生下一雌一雄，问一年后共有多少对兔子？”

分析:第一个月兔子没有繁殖能力,所以还是一对;两个月后生下一对兔子,共有两对;三个月后,老兔子生下一对,小兔子还没有繁殖能力,所以一共是三对,以此类推,可以列出如下数列：1, 1, 2, 3, 5, 8, 13, 21, 34, 55, 89, 144, 233，377，610，987，1597，2584，4181，6765，10946，17711，28657，46368........

c++程序

#include<iostream>

using namespace std;

int f(int n){
    if(n==2||n==1)return 1;
    return f(n-1)+f(n-2);        
}    

int main(){
    int num;
    num= f(24);
    cout << num ;
}

图解程序

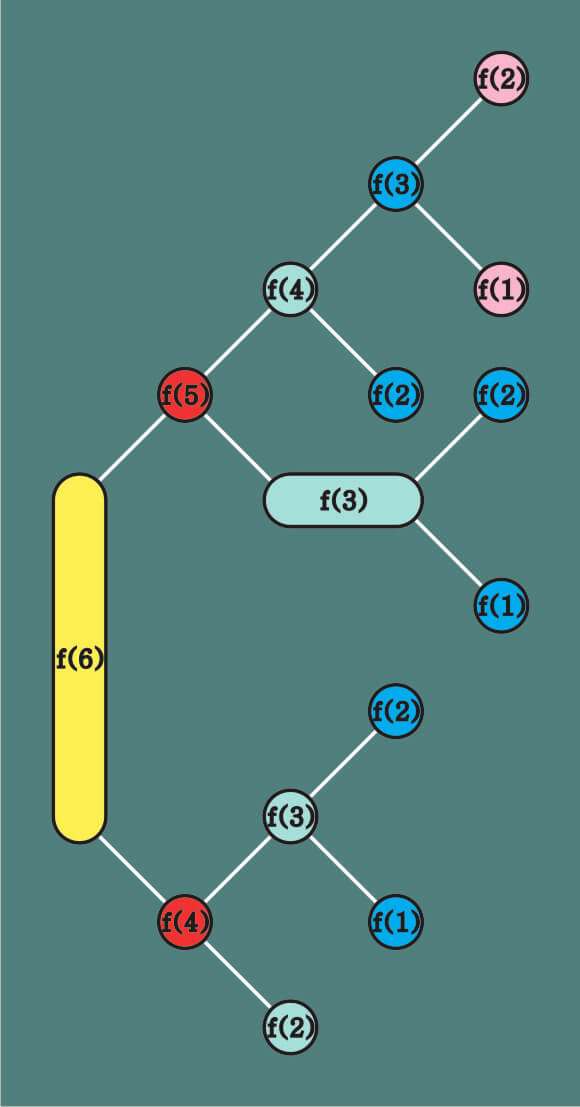
虽然只有短短两行程序，实际上程序做的事情可不少，假设是求斐波那契数列第6项的值，那么程序会返回“f(5)+f(4)”，这显然不是我们需要的实际数值，电脑也不会这么敷衍的将其返回，那么里面的函数f(5)+f(4)还会被继续执行，一直到运行到有具体返回值为止，计算第6项的计算步骤大致如下图。