在自然数的左边加上一个自然数，但该自然数不能超过原数的一半

NOIP2001普及组复赛题

输入一个自然数n，然后对此自然数按照如下方法进行处理：
（1）不作任何处理；
（2）在它的左边加上一个自然数，但该自然数不能超过原数的一半；（3）加上数后继续按此规则进行处理，直到不能再加自然数为止。

请找出以上操作能得到的数的个数，例如，n＝6时，满足条件的数为6个，分别为6、16、26、126、36、136.

输入格式

一行一个正整数n，n≤1000。

输出格式

一行一个整数，表示满足条件的数的个数。

输入样例

6

输出样例

6

完整程序

#include<iostream>

using namespace std;

int sum=1;

int chai(int n){
    if(n == 1){
        return 0;
    }else{
        for(int i=0;i<n/2;i++){
            sum++;
        chai(n/2-i);
        }
    }    
}

int main(){
    chai(8);
    cout<<sum<<endl;
}

程序思路

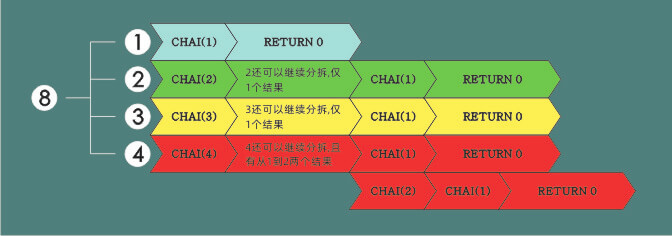
假设该自然数为8，那么不超过一半的数就是从1到4，也就是后续的10位允许有1，2，3，4这四种可能，除1之外，2、3、4都可以继续被拆分，所以我们实际解题的步骤是，取其一半，整理从1到该自然数一半的值，统计结果，继续取结果中的数（如还可以继续拆分），取其一半，统计结果。如果n为1，则程序返回。这里利用了一个循环，让递归产生了多路的分支，每一路分支依次sum++，程序运行完毕后的最终值，即可能产生结果的总和。

输出具体结果

上述的程序只是输出了统计结果，那么落实到实际数据究竟是哪几个结果呢，我们可以尝试在递归函数中定义一个用于存储的string变量result，利用它来直接输出结果：

#include<iostream>
using namespace std;

int digui(int n,string result){
    cout << result << endl;
    if(n/2==0)return 0;
    for(int i=1;i<=n/2;i++){
        digui(i,char(i+'0')+result);
    }
    return 0;
}


int main(){
    int a;
    string b;
    cin >> a;
    b=char(a+'0');
    digui(a,b);
}