P5788
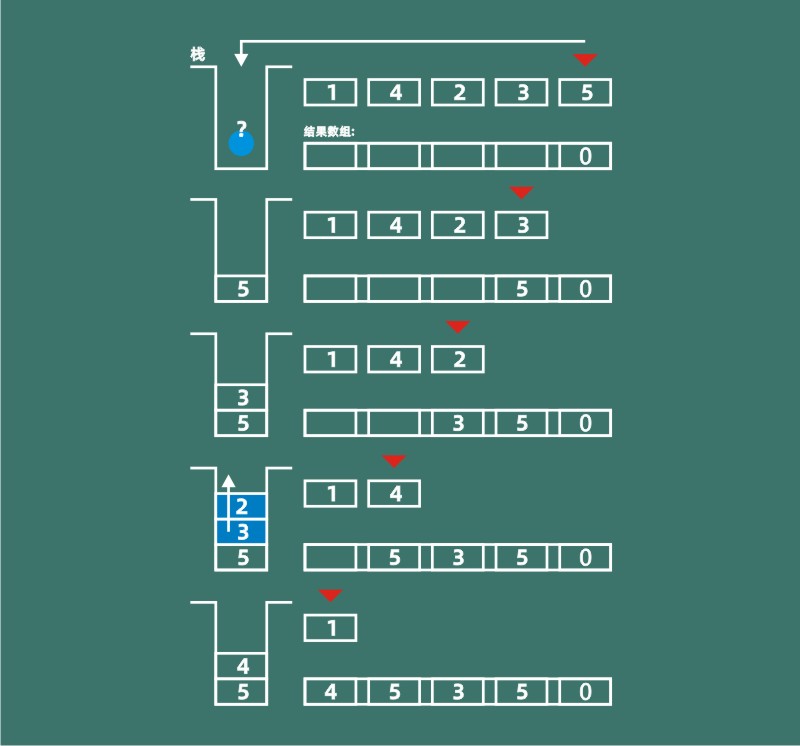
单调栈:初始化空栈存储下标,从右向左遍历数组,维护栈的单调递减性:当栈非空且当前元素大于等于栈顶元素时弹出栈顶,然后将当前下标入栈,此时栈顶即为当前元素右边第一个更大元素的位置(若栈空则记为0)。从右向左遍历能保证栈中元素均位于当前元素右侧且保持递减顺序。
P1057
传球游戏:万物皆可动态规划,偏偏万物都看不出来如何动态规划-_-!!!!因为可以左右互传,所以结果是左边一共有机会传过来几次加上右边一共有机会传过来几次,于是就有了状态转移方程:
//f[i][j]=f[i-1][j-1]+f[i-1][j+1]顺便贴一下完整的程序吧,虽然懂了,但可能也懂不了太久。
#include<iostream>
using namespace std;
const int MAXN=35;
int dp[MAXN][MAXN],n,m,l,r;
int main(){
cin >> n >> m;
dp[0][1]=1;
for(int i=1;i<=m;i++){
for(int j=1;j<=n;j++){
l = j - 1 ? j - 1 : n;
r = j < n ? j + 1 : 1;
dp[i][j]=dp[i-1][l]+dp[i-1][r];
}
}
cout << dp[m][1] << endl;
}B4184
除法运算:个人的思路是0到被除数开根号后取整之间的字段都是有效解,剩余利用循环判断。比如11开根号取整后为x=3,
所以0,1,2,3均为可能的解,然后在递减循环中去一下重:
for(i=x;i>=1;i--){...}P1479
宿舍里的故事之五子棋:需要注意的是这句话“只有这两种非负的 k 值,(注意 k 不重复),你要输出的便是 k 值的和。”,虽然给出的棋子可以任意放置,但如果只能连成一行的,都视为同种情况,比如给5个棋子,不管横放竖放斜着放,最多只能凑出一排5连,答案就是1。
P2426
删数:参考了第一个题解的程序,逻辑上有点看不太懂,所以在表格里模拟了一下流程:
原洛谷题解的程序:
#include <cstdio>
#include <algorithm>
using namespace std;
int n, val[105], dp[105];
inline int Val(int l, int r) {
return abs(val[l] - val[r]) * (r - l + 1);
}
int main(int argc, char const *argv[])
{
// freopen("nanjolno.in", "r", stdin);
// freopen("nanjolno.out", "w", stdout);
scanf("%d", &n);
for(int i = 1; i <= n; ++i) scanf("%d", &val[i]);
for(int i = 1; i <= n; ++i) {
dp[i] = max(dp[i], dp[i - 1] + val[i]);
for(int j = 2; j <= i; ++j)
dp[i] = max(dp[i], dp[i - j] + Val(i - j + 1, i));
}
printf("%d\n", dp[n]);
// fclose(stdin), fclose(stdout);
return 0;
}运行数据变化表格演示:
| 原数组 | 0 | 1 | 2 | 3 | 4 | 5 | 6 |
| val | 0 | 54 | 29 | 196 | 21 | 133 | 118 |
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=1 | 0 | 54 | 0 | 0 | 0 | 0 | 0 |
| j=2 不符合 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=2 | 0 | 54 | 83 | 0 | 0 | 0 | 0 |
| j=2 | |||||||
| dp[i-j]=dp[0] | |||||||
| Val(i - j + 1, i)=Val(1,2) | |||||||
| max(dp[2], dp[0] + Val(1, 2)) | |||||||
| 因为dp[0]=0, Val(1, 2)=50, 故最大值仍旧是83 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=3 | 0 | 54 | 83 | 388 | 0 | 0 | 0 |
| j=2 | |||||||
| dp[i-j]=dp[1] | |||||||
| Val(i - j + 1, i)=Val(2,3) | |||||||
| max(dp[3], dp[1] + Val(2, 3)) | |||||||
| 因为dp[1]=54, Val(2, 3)=334, 故最大值279被修改为388 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=3 | 0 | 54 | 83 | 426 | 0 | 0 | 0 |
| j=3 | |||||||
| dp[i-j]=dp[0] | |||||||
| Val(i - j + 1, i)=Val(1,3) | |||||||
| max(dp[3], dp[0] + Val(1, 3)) | |||||||
| 因为dp[0]=0, Val(1, 3)=426, 故最大值被修改为426 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=4 | 0 | 54 | 83 | 426 | 447 | 0 | 0 |
| j=2 | |||||||
| dp[i-j]=dp[2] | |||||||
| Val(i - j + 1, i)=Val(3,4) | |||||||
| max(dp[4], dp[2] + Val(3, 4)) | |||||||
| 因为dp[2]=83, Val(3, 4)=350, 故最大值447不变 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=4 | 0 | 54 | 83 | 426 | 447 | 0 | 0 |
| j=3 | |||||||
| dp[i-j]=dp[1] | |||||||
| Val(i - j + 1, i)=Val(2,4) | |||||||
| max(dp[4], dp[1] + Val(2, 4)) | |||||||
| 因为dp[1]=54, Val(2, 4)=24, 故最大值447不变 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=4 | 0 | 54 | 83 | 426 | 447 | 0 | 0 |
| j=4 | |||||||
| dp[i-j]=dp[0] | |||||||
| Val(i - j + 1, i)=Val(1,4) | |||||||
| max(dp[4], dp[0] + Val(1, 4)) | |||||||
| 因为dp[0]=0, Val(1, 4)=132, 故最大值447不变 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=5 | 0 | 54 | 83 | 426 | 447 | 650 | 0 |
| j=2 | |||||||
| dp[i-j]=dp[3] | |||||||
| Val(i - j + 1, i)=Val(4,5) | |||||||
| max(dp[5], dp[3] + Val(4, 5)) | |||||||
| 因为dp[3]=426, Val(4, 5)=224, 故最大值580被修改为650 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=5 | 0 | 54 | 83 | 426 | 447 | 650 | 0 |
| j=3 | |||||||
| dp[i-j]=dp[2] | |||||||
| Val(i - j + 1, i)=Val(3,5) | |||||||
| max(dp[5], dp[2] + Val(3, 5)) | |||||||
| 因为dp[2]=83, Val(3, 5)=189, 故最大值650不变 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=5 | 0 | 54 | 83 | 426 | 447 | 650 | 0 |
| j=4 | |||||||
| dp[i-j]=dp[1] | |||||||
| Val(i - j + 1, i)=Val(2,5) | |||||||
| max(dp[5], dp[1] + Val(2, 5)) | |||||||
| 因为dp[1]=54, Val(2, 5)=416, 故最大值650不变 | |||||||
| dp[0] | dp[1] | dp[2] | dp[3] | dp[4] | dp[5] | dp[6] | |
| i=5 | 0 | 54 | 83 | 426 | 447 | 650 | 0 |
| j=5 | |||||||
| dp[i-j]=dp[0] | |||||||
| Val(i - j + 1, i)=Val(1,5) | |||||||
| max(dp[5], dp[0] + Val(1, 5)) | |||||||
| 因为dp[0]=0, Val(1, 5)=395, 故最大值650不变 | |||||||
B3694
数列离散化:建议看看第一篇题解,提到了几个比较常用的函数,而本题就是一个比较好的练习。
//去重
unique(a+1,a+n+1)-(a+1);
//查索引
lower_bound(a+1,a+n+1,d[i])-a;CF847A
Union of Doubly Linked Lists:可以理解为把 l[0] r[0] 作为链表的起点。循环尝试找到一个无前导的链表段,如有就接到 r[0], 接下来去追查新找到的段落的终点 r[x], 我们的链表有了长度, 终点更新为了 r[x]。
B3631
单向链表:数组的下标用于存储值,数组空间用于存放下一个数的位置,初始数组为:
//初始
a[0]=1,a[1]=-1;
//99放在1后面
a[99]=a[1],a[1]=99;
//75方99后面
a[75]=a[99],a[99]=75;
//删除99后面的75
a[99]=a[a[99]];这道题的关键是题目中的这句话:“且保证任何时间表中所有数字均不相同”,才得以用类似桶排的思路完成搜索功能,完整代码如下:
#include <iostream>
using namespace std;
const int N= 1000005;
int n,a,x,y,nodes[N];
void init(int x){
nodes[0]=x;
nodes[x]=-1;
}
void addNode(int x,int y){
nodes[y]=nodes[x];
nodes[x]=y;
}
void removeNode(int x){
nodes[x]=nodes[nodes[x]];
}
int searchNode(int x){
return nodes[x]!=-1 ? nodes[x] : 0;
}
int main(){
cin >> n;
for(int i=0;i<n;i++){
cin >> a;
if(a==1){
cin >> x >> y;
addNode(x,y);
}else if(a==2){
cin >> x;
cout << searchNode(x) << endl;
}else if(a==3){
cin >> x;
removeNode(x);
}
}
}P1017
进制转换:被除数=商*除数+余数,这是解决问题的关键。例如在C++里:
-15%-2=-1,-15/-2=7,而7*-2+(-1)=-15但是因为我们是不断取余数倒序为转换结果,所以余数不能出现负数,那怎么办呢?我们只需要将商+1,余数-除数即可,因为余数(绝对值)一定小于除数,所以这样就可以将余数装换为正数,正确性证明:
(商+1)*除数+(余数-除数)=商*除数+除数+余数-除数=商*除数+余数=被除数P11242
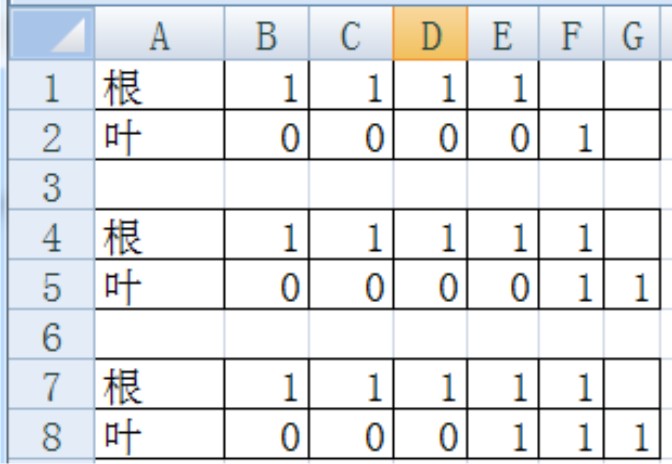
碧树:叶子越远,枝干越长,已有的枝干再长一片叶子不影响枝干长度,最终就是枝干的长度加上叶子的总数。枝干总长取决于最远的那片叶子,叶子的总数题目中已经提供。
P11248
矩阵移动:三层循环,最内层循环k表示分别修改0、1、2、3...个问号时的最优解。
参考程序:
#include <bits/stdc++.h>
using namespace std;
int t,n,m,x,dp[505][505][505];
string s[505];
int main(){
freopen("input.in","r",stdin);
freopen("input.out","w",stdout);
scanf("%d",&t);
while(t--){
scanf("%d%d%d",&n,&m,&x);
for(int i=1;i<=n;i++){
cin >> s[i];
s[i]=" "+s[i];
}
memset(dp,0,sizeof(dp));
for(int i=1;i<=n;i++){
for(int j=1;j<=m;j++){
for(int k=0;k<=x;k++){
dp[i][j][k]=(s[i][j]=='1')+max(dp[i-1][j][k],dp[i][j-1][k]);
if(k>0&&s[i][j]=='?')dp[i][j][k]=max(dp[i][j][k],1+max(dp[i-1][j][k-1],dp[i][j-1][k-1]));
cout << dp[i][j][k];
}
//cout << endl;
}
cout << endl << endl;
}
int ans=0;
for(int i=0;i<=x;i++)
ans=max(ans,dp[n][m][i]);
printf("%d\n",ans);
}
return 0;
}P1862
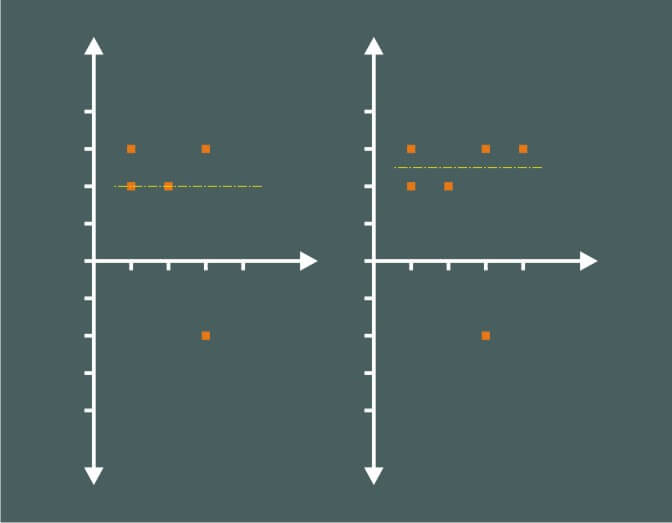
输油管道问题: 中位数又称中值,英语为Median,是按顺序排列的一组数据中居于中间位置的数,统计学中的专有名词,代表一个样本、种群或概率分布中的一个数值,其可将数值集合划分为相等的上下两部分。对于有限的数集,可以通过把所有观察值高低排序后找出正中间的一个作为中位数。如果观察值有偶数个,通常取最中间的两个数值的平均数作为中位数。
因为平均数容易受到极端数值的影响,比如国民生产总值,又比如一个公司的平均收入,领导层可能占据了收入的大头,人均后几万的收入并不能准确描述一个公司的普通员工收入。在这道题目中,排序找到中位,然后以中位为中心,累计首尾相减差值即可。
P11308
| 队伍数 | 队伍上限 | 小队 | 已分配 | 均值(已分配/队伍数) |
| 3 | 3 | 3 | 1 | 0 |
| 3 | 3 | 4 | 5 | 1 |
| 4 | 4 | 4 | 12 | 3 |
| 4 | 4 | 3 | 8 | 2 |
| 10 | 10 | 7 | 34 | 3 |
| 10 | 10 | 8 | 34 | 3 |
| 12 | 11 | 11 | 12 | 1 |
| 12 | 11 | 12 | 12 | 1 |
| 9 | 9 | 1 | 80 | 8 |
| 9 | 9 | 6 | 70 | 7 |
茫茫的不归路: 小队人数大于队伍上限,则必然为“Divide”,接下来取一个均值(向下取整),均值人数平均分配时,可插入人数最多的情况,如最差情况时,均值加拟插入小队的总和仍不超过队伍上限,则为“Together”,否则就只能是听天由命的“Chance”了。