csp-j中需要知道的c++数学运算知识

最大公约数最小公倍数

以辗转相减的方式：

#include <iostream>

// 辗转相除法计算最大公约数
int gcd(int a, int b) {
    if (b == 0) {
        return a;
    } else {
        return gcd(b, a % b);
    }
}

// 最小公倍数 = 两数之积 / 最大公约数
int lcm(int a, int b) {
    return (a * b) / gcd(a, b);
}

int main() {
    int num1 = 4;
    int num2 = 6;
    int result = lcm(num1, num2);
    std::cout << "最小公倍数为: " << result << std::endl;
    return 0;
}

三角形面积

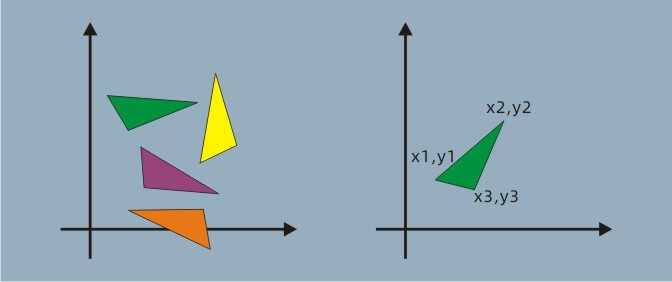
在坐标系中任意取3个点组成一个三角形，求这个三角形的面积，可以考虑将其中一个点移动到原点，然后将剩下两个点坐标交叉相乘后相减，取绝对值：

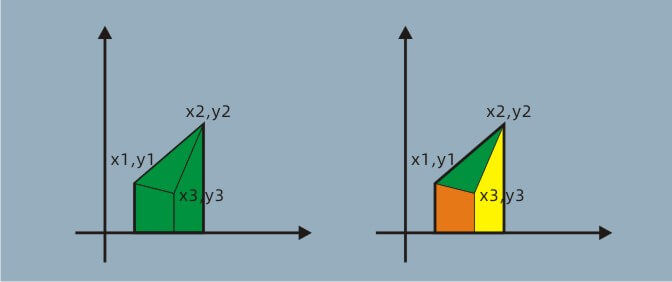
试着画图求证了一下：

最大梯形面积:
(x2-x1)(y1+y2)    
=x2y1+x2y2-x1y1-x1y2

两个需要减掉的梯形面积:
(x3-x1)(y1+y3)
=x3y1+x3y3-x1y1-x1y3

(x2-x3)(y2+y3)
=x2y2+x2y3-x3y2-x3y3

(x2-x1)(y1+y2)-(x3-x1)(y1+y3)-(x2-x3)(y2+y3)
=x2y1-x1y2-x3y1+x1y3-x2y3+x3y2

当其中某点为原点(0,0)的时候,我们假设3号点位于原点,上面的公式可以简化为:
=x2y1-x1y2

统计方形问题

∵ 矩形长不等于宽
∴ 子矩形构成的矩阵的长宽是由原矩形长宽减去不同数而得
即(n-b)*(m-a) (a≠b)

∵正方形长等于宽
∴子正方形构成的矩阵的长宽由原矩形长宽减去相同数而得
即(n-b)*(m-a) (a=b)

#include<iostream>
using namespace std;

long long n,m,re,sq;

int main(){
    cin >> n >> m;
    for(int i=0;i<n;i++){
        for(int j=0;j<m;j++){
            i==j ? sq+=(n-i)*(m-j) : re+=(n-i)*(m-j);
        }
    }
    cout << sq << " " << re;
}

素数筛选

欧拉筛：

#include<iostream>
using namespace std;

bool num[10001];
int pri[10001];

int check(int n){
    int top=0;
    for(int i=2;i<=n;i++){
        if(num[i]==false){
            pri[top++]=i;
        }
        for(int j=0;j<top;j++){
            if(i*pri[j]>n)break;
            num[i*pri[j]]=1;
            if(i%pri[j]==0)break;
        }
    }
    return top;
}

int main(){
    cout<< pri[check(100)-1];
}