在oiwiki学习01背包,虽然完成并通过了题目(洛谷P2871),但总感觉似懂非懂,干脆在画图软件上推演了一下,于是就有了这篇笔记。所谓01背包,一般是给定一个固定容量的容器(背包),并提供固定件数的物品,每件物品有各自的体积(或称重量)与价值,每件物品仅允许使用一次,要求做题者求出装满背包后的最大价值。比如下面这道P2871的例题:
有 $N$ 件物品和一个容量为 $M$ 的背包。第 $i$ 件物品的重量是 $W_i$,价值是$D_i$。求解将哪些物品装入背包可使这些物品的重量总和不超过背包容量,且价值总和最大。
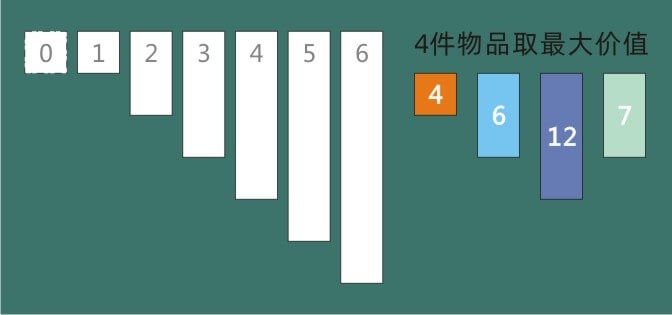
将洛谷示例数据绘制如上图,左侧为数组,因为数组的下标被利用为了容器的容积,所以根据下标的大小,将数组图形化为了容积递增的容器。右侧是4个物品,比如第一个物品重量是1,价值是4,同数组一样,重量同样也被图形化为了尺寸差异。
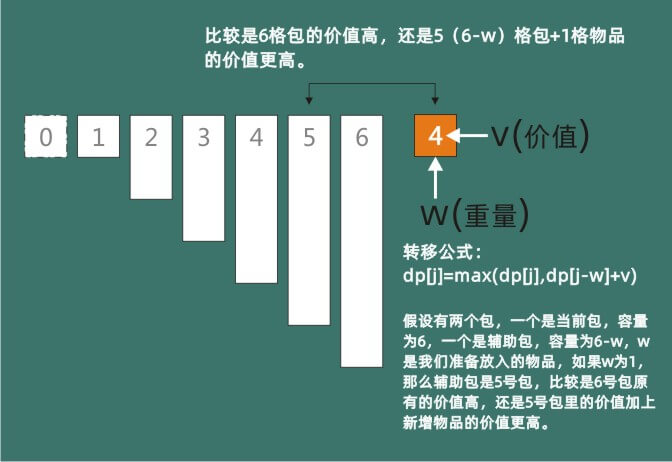
状态转移方程,是动态规划的关键,在这道题目中,我们会逆序依次向数组中放入当前物品,但放置之前,我们需要判断一下,是原有单元格的价值更高,还是把当前物品放进去之后价值更高。这个比较中需要一个辅助格,辅助格号就是当前容积的数组单元格号,减去当前物品的重量。
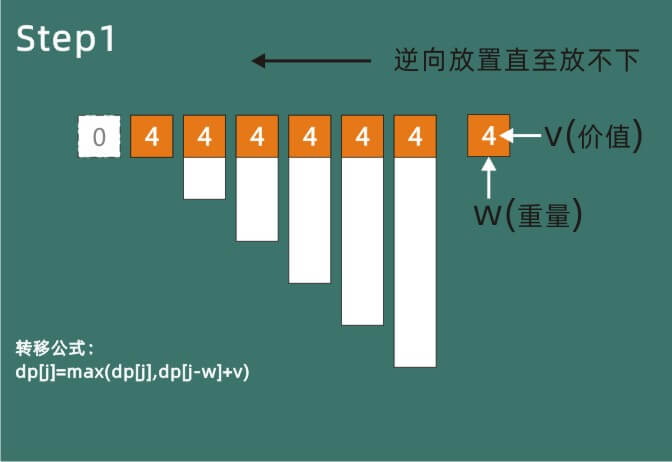
实际来放置一下更为直接观一些,因为数组的初值均为0,所以第一个物品放入时并不会真正产生不放的状态。
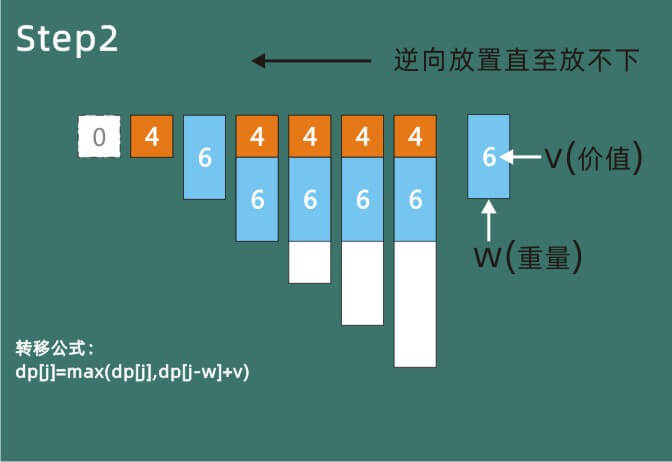
从第二个开始,辅助格子里开始有了数据。下标为2的数组中原来放置的是物品1,价值为4,显然要小于当前价值6的物品加上0号背包的价值,所以被替换掉了。
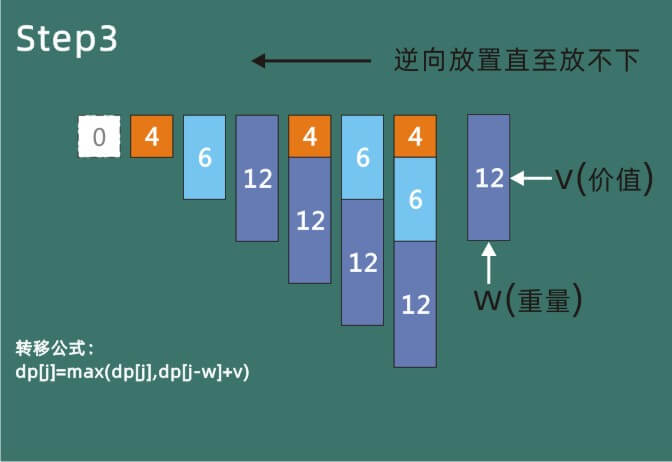
后续的过程逻辑相同,需要注意的是,01背包的物品摆放需要逆序执行,顺序执行的话,当前单元格的数据一旦发生变动,当当前单元格作为辅助格时,这个数据就不准确了,会影响到最终的结果。
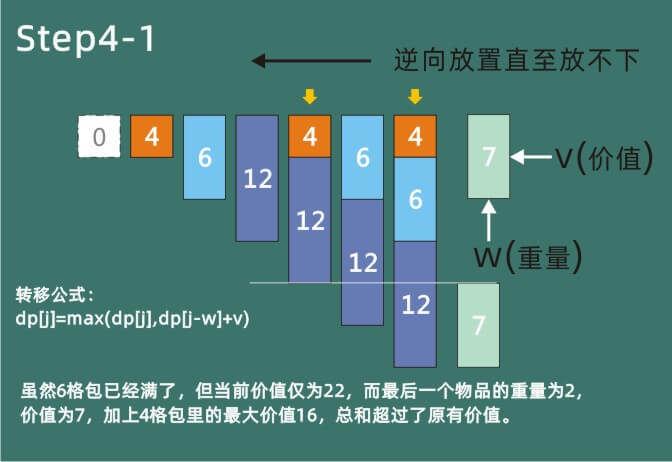
这里博主添加了一条辅助线,可以直观的看到,当前物品为7时,重量为2,加上数组4号辅助格的价值后,会大于原有的6格包的价值。

替换最终结果如上,当前示例的最大价值为23。
完整程序
#include<iostream>
using namespace std;
int n,m,w[12901],v[12901],dp[12901];
int main(){
cin >> n >> m;
for(int i=0;i<n;i++){
cin >> w[i] >> v[i];
}
for(int i=0;i<=n;i++){
for(int j=m;j>=w[i];j--){
dp[j]=max(dp[j],dp[j-w[i]]+v[i]);
}
}
cout << dp[m] << endl;
return 0;
}类似题目
P1216 数字三角形:异形二维数组
P1802 5 倍经验日:双重条件
P1507 NASA的食物计划:标准二维动态规划

