上节我们尝试了利用Scratch的递归方法,这一节我们继续利用递归来完成一个求和运算,递归是一种在自制积木(函数)中嵌套自制积木(函数)的方法,类似于在一个排列整齐的队伍中强行插入了另一列队伍(现实生活中的插队不可取哦),并且要求程序按新的队列执行。有时候我们并不深究程序究竟循环多少次,只要求特定的值跑到位即可,类似这种情况,我们就可以考虑递归的方式。
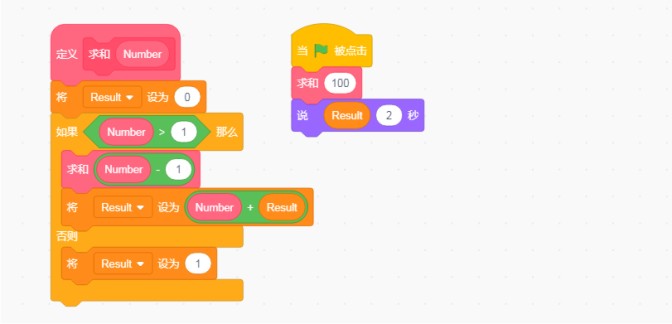
上面这个程序实现了一个“1+2+3+4...”这样的算式的求值,如果把求和积木的参数项填充为100,则是计算“1+2+3+...+100”的值。恩...显然结果是5050,聪明的你可能已经连答案都已经会背了。
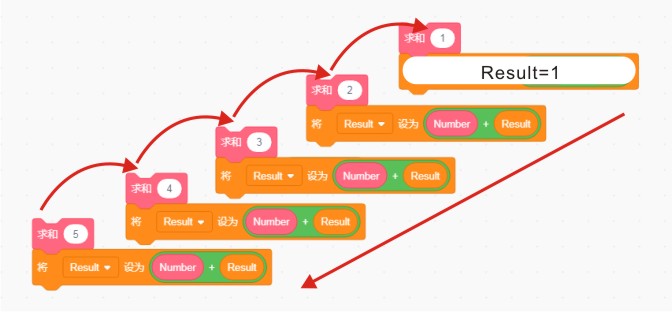
当“求和(5)”的时候,我们可以把题目理解为“5+求和(4)”,而当“求和(4)”的时候,我们可以依次类推把题目理解为“4+求和(3)”,当“求和(1)”的时候我们就不推了,直接摊牌了,把Result设置为1,因为插队大法的存在,当我们真正计算Number+Result的值的时候,Result不偏不倚刚好是我们所需要的值。
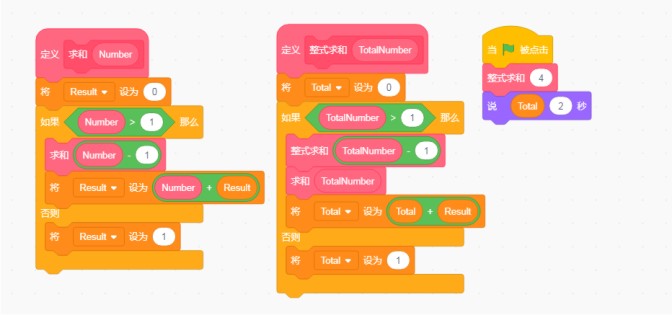
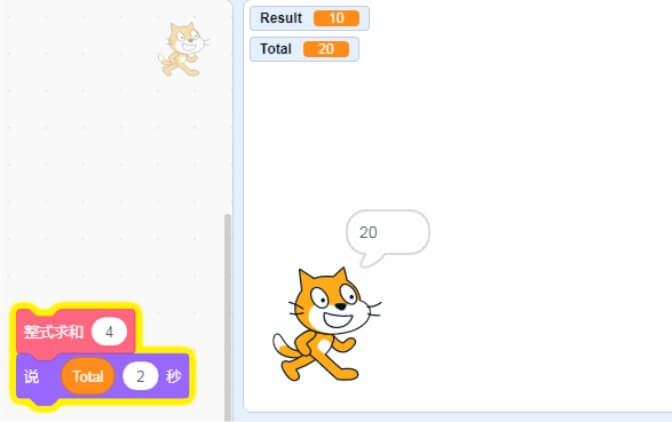
可不仅仅用来求和哦,我们还可以进行一些更复杂的操作,比如来求和一个类似下方的整式:
1+(1+2)+(1+2+3)+(1+2+3+4)是不是感觉抽象又神奇呢,亲也一起来试试吧。